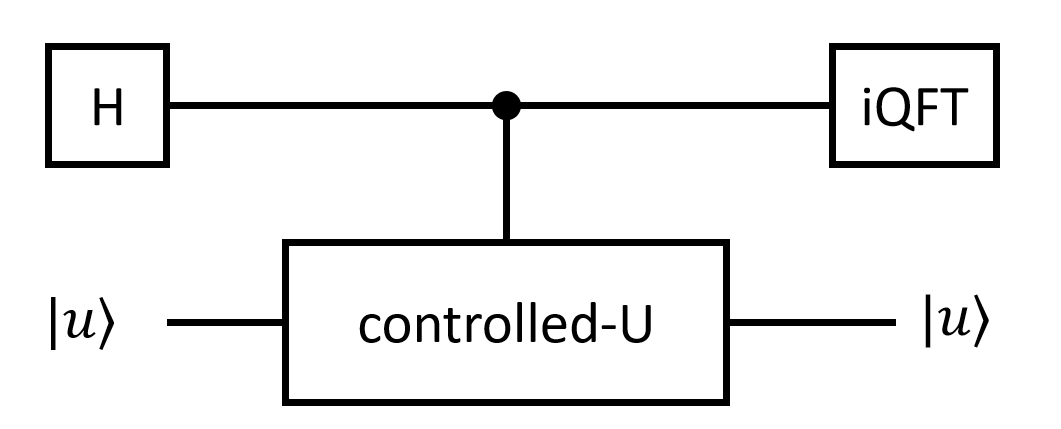
Phase Estimation

由于对于任何幺正变换$U$我们有
$$U|u\rangle=e^{i\theta }|u\rangle.$$
其中$0\leq \theta < 2\pi$。

现在重新将$\theta$映射到整数，定义$\phi=N\theta/2\pi$为一个n位二进制数（范围$[0,N)$, $N=2^n$），则我们可以将上式重新写为

$$U|u\rangle=e^{2\pi i\phi/N }|u\rangle.$$

• 注意到这里$\phi$只是“假设”为一个整数
• 接下来我们推导过程中先按照$\phi$为整数处理

到Controlled-U为止做了什么

从上往下，定义为第0位，第1位，第2位……

$$ c-U(|0\rangle|u\rangle+|1\rangle|u\rangle)=|0\rangle|u\rangle + e^{2\pi i\phi/N }|1\rangle|u\rangle=\sum_{z=0}^{1}e^{2\pi i\phi/N z }|z\rangle|u\rangle. $$

$$ \begin{aligned} &\sum_{z_2,z_1,z_0}|z_2z_1z_0\rangle\otimes |u\rangle\\ \rightarrow &\sum_{z_2,z_1,z_0}|z_2z_1z_0\rangle e^{(2\pi i\phi/N) z_0}|u\rangle\\ \rightarrow &\sum_{z_2,z_1,z_0}|z_2z_1z_0\rangle e^{(2\pi i\phi/N) z_0}e^{(2\pi i\phi/N) 2z_1}|u\rangle\\ \rightarrow &\sum_{z_2,z_1,z_0}|z_2z_1z_0\rangle e^{(2\pi i\phi/N) z_0}e^{(2\pi i\phi/N) 2z_1}e^{(2\pi i\phi/N) 4z_2}|u\rangle\\ \rightarrow&...\\ \rightarrow&\sum_{z=0}^{2^n-1}|z\rangle e^{(2\pi i\phi/N) z}|u\rangle\\ =&\sum_{z=0}^{2^n-1}e^{(2\pi i\phi/N) z}|z\rangle\otimes |u\rangle \end{aligned} $$

其中$z$的二进制表示为$\overline{z_{n-1}...z_2z_1z_0}$

QFT和iQFT

QFT

QFT实现下述变换

$$ |x\rangle\mapsto\sum_{y=0}^{2^n-1}e^{2\pi ixy/N}|y\rangle $$

这里$x,y$同为$n$位自然数，$xy/N$均为正常的自然数乘除。另一种写法是

$$ |x\rangle\mapsto\sum_{y=0}^{2^n-1}\omega^{xy}|y\rangle $$

其中$\omega=e^{2\pi i/N}$

根据之前的惯例，可以把QFT对应的矩阵写出来

$$ \begin{aligned} U_{\mathrm{QFT}}&=\sum_{x=0}^{2^n-1}\left(\sum_{y=0}^{2^n-1}e^{2\pi ixy/N}|y\rangle\right)\langle x|\\ &=\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1}e^{2\pi ixy/N}|y\rangle\langle x| \end{aligned} $$

可以发现它构成了一个$(x,y)$矩阵元恰好为$e^{2\pi ixy/N}$的矩阵.

• QFT具有对称性

iQFT

iQFT是QFT的逆，即$U_{\mathrm{iQFT}}=U_{\mathrm{QFT}}^\dagger$，因此我们有

$$ U_{\mathrm{iQFT}}=\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1}e^{-2\pi ixy/N}|y\rangle\langle x| $$

• 对称矩阵的转置共轭？

相位估计 Phase estimation

$\sum_{z=0}^{2^n-1} e^{(2\pi i\phi/N) z}|z\rangle$经过$U_{\mathrm{iQFT}}$之后得到

$$ \begin{aligned} &\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1}e^{2\pi ixy/N}|y\rangle\langle x|\sum_{z=0}^{2^n-1} e^{-2\pi i\phi z/N }|z\rangle\\ =&\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1}\sum_{z=0}^{2^n-1}e^{2\pi ixy/N-2\pi i\phi z/N}|y\rangle\langle x|z\rangle\\ =&\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1}\sum_{z=0}^{2^n-1}e^{2\pi ixy/N-2\pi i\phi z/N}|y\rangle\delta_{xz}\\ =&\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1}e^{2\pi ixy/N-2\pi i\phi x/N}|y\rangle \end{aligned} $$

简单代换$\omega=e^{2\pi i/N}$后，并且整理，可得

$$ \begin{aligned} &\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1}\omega^{xy-x\phi }|y\rangle\\ =&\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1}\omega^{x(y-\phi) }|y\rangle\\ =&\sum_{y=0}^{2^n-1}\sum_{x=0}^{2^n-1}\omega^{x(y-\phi) }|y\rangle \end{aligned} $$

怎么理解这个输出态？

1. 先理解符号的定义

• $x,y,\phi$: 都是某个整数
• $|y\rangle$ 是$y$这个整数对应的量子态
• $\sum_{x=0}^{2^n-1}\omega^{x(y-\phi) }$是其中一个$|y\rangle$分量的振幅，它每项是个模为1的复数，相位为$\omega$相位的$x(y-\phi)$倍，即$$x(y-\phi)\frac{2\pi}{N}$$

• 输出态
  $$\sum_{y=0}^{2^n-1}\sum_{x=0}^{2^n-1}\omega^{x(y-\phi) }|y\rangle$$
  是对于上面所有$|y\rangle$的求和，因此整个输出态可以写成下述的矢量形式

  $$ \frac{1}{N} \begin{pmatrix} \sum_{x} \omega ^{x(0-\phi)}\\ \sum_{x} \omega ^{x(1-\phi)}\\ \sum_{x} \omega ^{x(2-\phi)}\\ \vdots\\ \sum_{x} \omega ^{x(2^n-2-\phi)}\\ \sum_{x} \omega ^{x(2^n-1-\phi)} \end{pmatrix} $$

  • 为什么归一化常数为$1/N$？ （显然）

2. 测量这个量子态，得到每个态的概率可以写为

$$p_y = \frac{1}{N^2}|\sum_{x=0}^{2^n-1}\omega^{x(y-\phi) }|^2$$

先考虑一个特殊情况，即 $p_{y=\phi}$

$$ \begin{aligned} p_{y=\phi} &= \frac{1}{N^2}|\sum_{x=0}^{2^n-1}\omega^{0 }|^2\\ &=1 \end{aligned} $$

利用排除法可知$p_{y\neq\phi}=0$，因此上面的量子态是这个形式

$$ \begin{pmatrix} 0\\ 0\\ 0\\ \vdots\\ 1\\ \vdots\\ 0\\ 0 \end{pmatrix}=|\phi\rangle $$

思考题：如何推导出$\sum_{x=0}^{2^n-1}\omega^{x(y-\phi) }=0$ 其中$y\neq\phi$？

• 提示1. 等比数列求和
• 提示2. 关于原点对称的复数之和为0，或者说相位恰好差$\pi$的复数之和为0
• 提示3. $\omega^N=1,\omega^{N/2}=-1$

小结

相位估计通过$U$作为子过程，实现了如下的变换
$|0\rangle|u\rangle \mapsto |\phi\rangle|u\rangle$
其中$\phi$和$U$在$|u\rangle$上的本征值相关，具体来说有$U|u\rangle=e^{2\pi i\phi/N}|u\rangle$.

• $\phi$为一个$n$位整数，有$N=2^n$

Query complexity 访问复杂度

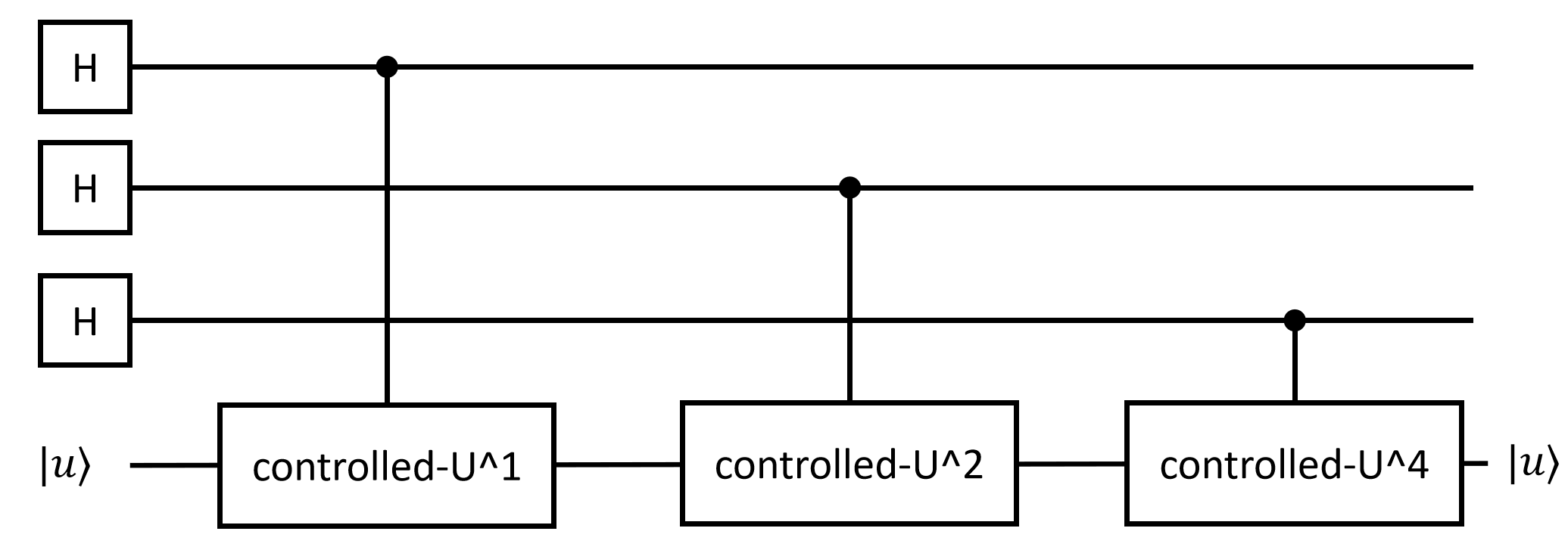
当我们认为$H$和$\rm iQFT$是较为固定的过程时，实现Phase Estimation的主要复杂度集中于control-U上。这代表我们需要执行$Control-U^k$多少次决定了算法的实际复杂度。描述这种“调用其他子过程X次”的复杂度，称作算法对于U的访问复杂度(query complexity)。

具体来说，依次实现$c-U$, $c-U^2$, ...$c-U^{2^n}$，存在两种可能性

1. 实现$c-U$和$c-U^t$的复杂度无明显关系

   • 此时query complexity为$O(\log N)$, 其中$N=2^n$，$n$为表示$\phi$的位数
   • 假设我们称$\epsilon$为相位$\phi$的精度，即$\epsilon=\frac{1}{N}$，那么query complexity为$O(\log 1/\epsilon)$

2. 实现$c-U^t$等于重复$t$次$c-U$

   • 此时query complexity为$O(N)$，用精度$\epsilon$表示的话，写为$O(1/\epsilon)$

Amplitude estimation (Quantum counting)

在Grover和amplitude amplification中提到了一类问题

$$U|0,0\rangle = \sqrt{p_\mathrm{succ}}|\mathrm{good}\rangle|0\rangle+\sqrt{1-p_\mathrm{succ}}|\mathrm{bad}\rangle|1\rangle$$

需要$O(1/p_\mathrm{succ})$次放大来以较高概率制备$|\mathrm{good}\rangle$，现在的问题是如何确定$p_{\rm succ}$？因为若不知道这个具体概率，我们无法选择需要执行Amplitude amplification循环的次数。

回顾Amplitude amplification

我们选择$|\mathrm{good}\rangle|0\rangle$和$|\mathrm{bad}\rangle|1\rangle$子空间，定义算符
$$ U_O=2|\mathrm{good},0\rangle\langle \mathrm{good},0|-I $$

$$ \begin{aligned} U_S&=U(2|0,0\rangle\langle 0,0|-I)U^\dagger \\ &=2|\psi\rangle\langle \psi|-I \end{aligned} $$

$U_OU_S$因此构成了在$|\mathrm{good}\rangle|0\rangle$和$|\mathrm{bad}\rangle|1\rangle$子空间上的一组旋转变换。

$$ \begin{pmatrix} 1-2/N & -2\sqrt{N-1}/N \\ 2\sqrt{N-1}/N & 1-2/N \end{pmatrix}=\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}, $$

这使得我们可以从$\sin\alpha|\mathrm{good}\rangle|0\rangle+\cos\alpha|\mathrm{bad}\rangle|1\rangle$变换到$\sin(\alpha+n\theta)|\mathrm{good}\rangle|0\rangle+\cos(\alpha+n\theta)|\mathrm{bad}\rangle|1\rangle$

一开始$\sin\alpha$很小，对应成功率很小的情况，每走一步，都可以让成功率对应的角度上升$\theta\sim \arcsin \sqrt {p_\mathrm{good}}\sim \sqrt{p}$。由于$n\theta\sim \pi/2$所需的$n=O(1/\sqrt {p_\mathrm{good}})$，这对应了我们需要进行振幅放大的步骤。

从振幅放大到振幅估计

别忘了，振幅放大的算符仍然是一个幺正算符，即$U=U_OU_S$，因此也存在某一组$|u\rangle$满足上面所说的

$$U|u\rangle = e^{-2\pi i\phi/N}|u\rangle$$

• 如何确定$|u\rangle$？

容易找到在子空间上的$|u\rangle$！即直接对下面的矩阵进行本征分解

$$ \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} $$

简单列一个求本征值的方程

$$ |\lambda I-U| = \left| \begin{matrix} \lambda-\cos \theta & \sin \theta \\ -\sin \theta & \lambda-\cos \theta \end{matrix}\right|=0 $$

解得

$$ \lambda_1=e^{-i\theta}, |u_1\rangle=\frac{1}{\sqrt{2}}\begin{pmatrix} 1\\ i \end{pmatrix} $$

$$ \lambda_2=e^{i\theta}, |u_2\rangle=\frac{1}{\sqrt{2}}\begin{pmatrix} 1\\ -i \end{pmatrix} $$

通过$\cos\theta\pm i\sin\theta=e^{\pm i\theta}$可以简单验证。

从子空间的观点来看$|u_1\rangle=\frac{1}{\sqrt 2}(|\mathrm{good}\rangle|0\rangle+i|\mathrm{bad}\rangle|1\rangle)$, $|u_2\rangle=\frac{1}{\sqrt 2}(|\mathrm{good}\rangle|0\rangle-i|\mathrm{bad}\rangle|1\rangle)$

振幅估计 = 将振幅放大算子$U_SU_O$作为相位估计的算子$U$

我们考察这个过程，不妨假设下方输入态$|u\rangle$改为$|\psi\rangle=\sqrt{p_\mathrm{succ}}|\mathrm{good}\rangle|0\rangle+\sqrt{1-p_\mathrm{succ}}|\mathrm{bad}\rangle|1\rangle$，因为后者容易制备。

容易发现 $|\psi\rangle$显然也是$|u_1\rangle$和$|u_2\rangle$的线性组合，即

$$ \begin{aligned} |\psi\rangle&=\sqrt{p_\mathrm{succ}}\frac{1}{\sqrt{2}}(|u_1\rangle+|u_2\rangle)+\sqrt{1-p_\mathrm{succ}}\frac{1}{\sqrt{2i}}(|u_1\rangle-|u_2\rangle)\\ &=(\sqrt{p_\mathrm{succ}}-i\sqrt{1-p_\mathrm{succ}})|u_1\rangle+(\sqrt{p_\mathrm{succ}}+i\sqrt{1-p_\mathrm{succ}})|u_2\rangle\\ &=C_1|u_1\rangle+C_2|u_2\rangle \end{aligned} $$

现在执行振幅估计，由于我们上面已经计算了$U_SU_O$的本征态和本征值，那么我们可以写出

$$ \begin{aligned} &|0\rangle\otimes (C_1|u_1\rangle+C_2|u_2\rangle)\\ =&C_1|0,u_1\rangle+C_2|0,u_2\rangle\\ \rightarrow&C_1|\tilde{\lambda_1},u_1\rangle+C_2|\tilde{\lambda_2},u_2\rangle \end{aligned} $$

其中$\tilde{\lambda_1}$是一个整数，对应了$N\lambda_1/2\pi$的整数部分；$\tilde{\lambda_2}$同理

当我们测量第一个寄存器时，上面的值有两种情况：$\tilde{\lambda_1}$，$\tilde{\lambda_2}$。通过$2\pi \tilde{\lambda_i}/N$计算出的结果对应了$\theta$或$2\pi-\theta$。由于$\theta\sim \sqrt p$，是个很小的数，不论如何我们都能寻找到对应的结果。

思考题

1. 这个算法的精度和$\sqrt{p}$之间的关系
2. 这个算法的访问复杂度(query complexity)是多少？

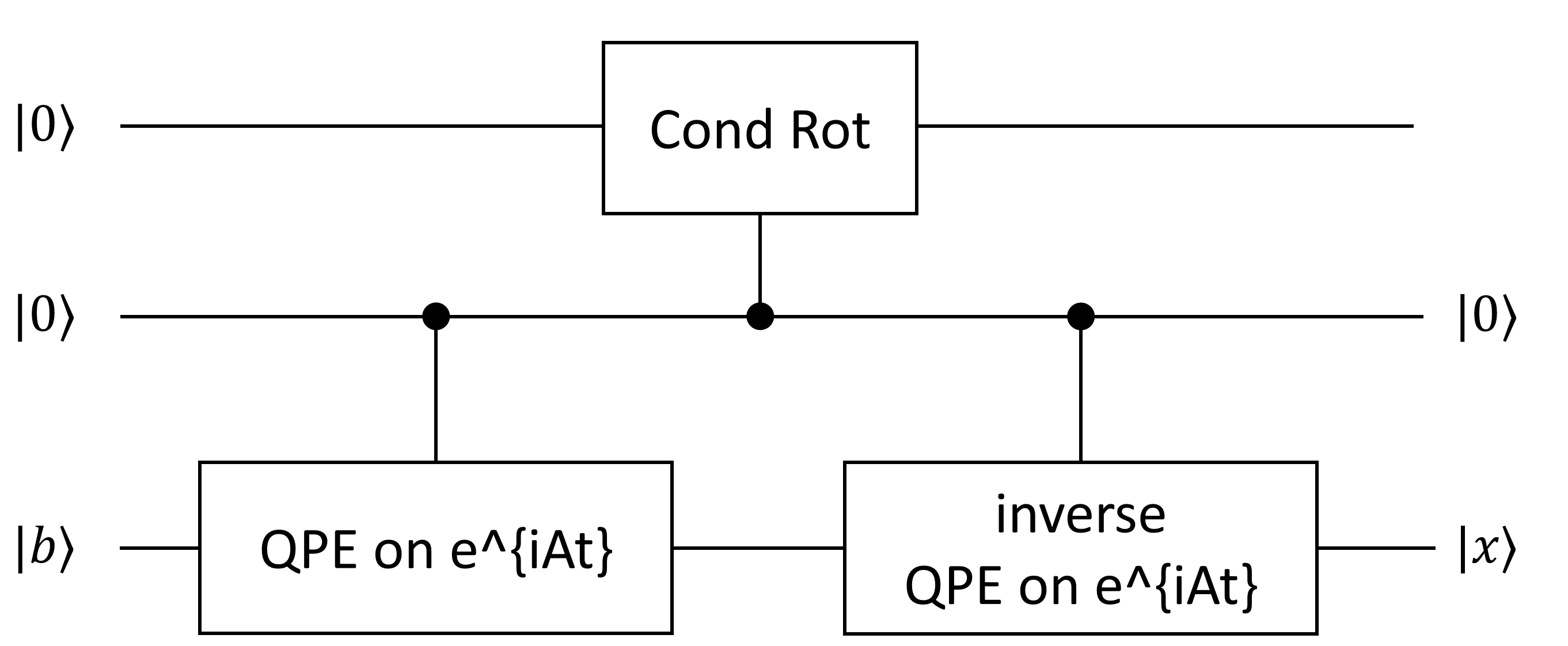
HHL算法，对矩阵进行本征分解实现求逆

线性求解$Ax=b$，即找到$x=A^{-1}b$，其量子版本描述如下

• 给出厄密Hermitian矩阵$A$，假设我们能实现$U=e^{iAt}$，其中$t$是某实数；假设拥有输入态$|b\rangle$，目标是制备
  $$|x\rangle=A^{-1}|b\rangle/\|A^{-1}|b\rangle\|_2.$$
  其中$1/\|A^{-1}|b\rangle\|_2$为归一化常数。

对$U=e^{iAt}$的本征分解

1. $U=e^{iAt}$和$A$具有相同的本征态

不妨设$A|u_i\rangle=\lambda_i|u_i\rangle$，显然也有$A^n|u_i\rangle=\lambda_i^n|u_i\rangle$，那么也可以写出

$$e^{iAt}|u_i\rangle=e^{i\lambda_i t}|u_i\rangle$$

显然我们根据$A$的本征态和本征值知道了$U=e^{iAt}$的本征态和本征值

2. 计算$x=A^{-1}b$

$$A^{-1}|u_i\rangle = \lambda_i^{-1}|u_i\rangle$$

我们可以把$|b\rangle$写成$|u_i\rangle$的线性组合

$$|b\rangle=\sum_i b_i|u_i\rangle$$

因此我们有$A^{-1}|b\rangle=b_i\lambda_i^{-1}|u_i\rangle$

3. 算法

Step 1. 对$|0\rangle\otimes |b\rangle$执行关于$e^{iAt}$的相位估计

这里我们可以把输入态重新写成关于$e^{iAt}$本征态的线性组合

$$|b\rangle = \sum_i b_i|u_i\rangle$$

因此执行了这一步操作之后生成的量子态为

$$ \begin{aligned} |0\rangle\otimes|b\rangle &= \sum_i b_i|0,u_i\rangle\\ &\rightarrow \sum_i b_i|\lambda_i,u_i\rangle \end{aligned} $$

$\lambda_i$是一个和$|u_i\rangle$在$U$上的本征值相关的一个整数（正比于这个本征值）。

Step 2. 执行Conditional Rotation，它是一个受控的单比特操作，将$|0,\lambda_i\rangle$变为

$$ (\frac{C}{\lambda_i}|0\rangle + \sqrt{1-\frac{C^2}{\lambda_i^2}}|1\rangle )|\lambda_i\rangle $$

其中$C$是某常数$0<C\leq\max \lambda_i$

总的量子态变为

$$ \begin{aligned} |0\rangle\otimes\sum_i b_i|\lambda_i,u_i\rangle&=\sum_i b_i|0,\lambda_i,u_i\rangle\\ &\rightarrow \sum_i b_i(\frac{C}{\lambda_i}|0\rangle+ \sqrt{1-\frac{C^2}{\lambda_i^2}}|1\rangle )|\lambda_i,u_i\rangle\\ \end{aligned} $$

Step 3. 执行QPE操作的逆，也就是Step 1的逆，这恰好能

$$ \begin{aligned} &\sum_i b_i|\lambda_i,u_i\rangle\\ \rightarrow& \sum_i b_i|0,u_i\rangle\\ \end{aligned} $$

则最终量子态变为

$$ \sum_i b_i(\frac{C}{\lambda_i}|0\rangle+ \sqrt{1-\frac{C^2}{\lambda_i^2}}|1\rangle )|0,u_i\rangle $$

此时第二个寄存器固定为$|0\rangle$，不再关注它，只关注1、3号寄存器，我们有

$$ \begin{aligned} &\sum_i b_i(\frac{C}{\lambda_i}|0\rangle+ \sqrt{1-\frac{C^2}{\lambda_i^2}}|1\rangle )|u_i\rangle\\ =&|0\rangle\otimes\sum_i C\frac{b_i}{\lambda_i}|u_i\rangle+ |1\rangle\otimes\sum_ib_i\sqrt{1-\frac{C^2}{\lambda_i^2}}|u_i\rangle \end{aligned} $$

由于我们知道$|x\rangle = D\sum_ib_i\lambda_i^{-1}|u_i\rangle$,上面的量子态可以进一步整理为

$$\sqrt{p}|0,x\rangle+\sqrt{1-p}|1,\mathrm{bad}\rangle$$

其中$\sqrt{p}=C/D$, $C$和$D$均为常数。

• 算法有$p$的成功率
• 当第一个寄存器测到$|0\rangle$时，第二个寄存器上恰好就是我们想要的态，即线性求解的结果$|x\rangle$

思考题

1. 怎么进一步将HHL算法结合到amplitude estimation和amplitude amplification上？
2. 为什么量子线性求解器存在成功概率？HHL算法中为什么我们要选择$C$？选择$C=1$的劣势是什么？
3. 阅读QCQI和论文，说明Phase estimation在选取不同精度时，对算法效果和运行时间的影响。如何解决$N\phi/2\pi$不是整数的情况，最后产生了什么结果？